Vertical Curve หรือโค้งดิ่ง เป็นโค้งพาราโบล่าที่ใส่เข้าไปในช่วงที่เส้นตัดเกรดงานระดับถนนตัดกันเพื่อให้การขับขี่ยานพาหนะปลอดภัยมากขึ้น
โค้งดิ่งนี้แบ่งออกเป็นสองชนิด คือ
- โค้งชนิดสมมาตร Symmetrical Curve คือโค้งที่มีระยะจาก sta PVC ถึง sta PVI เท่ากับระยะจาก sta PVI ถึง sta PVT (l1 = l2)
- โค้งชนิดไม่สมมาตร Unsymmetrical Curve คือโค้งที่มีระยะจาก sta PVC ถึง sta PVI ไม่เท่ากับระยะจาก sta PVI ถึง sta PVT (l1 ≠ l2)
และโค้งทั้งสองชนิดนี้ยังแบ่งตามการวางตัวของโค้งออกเป็นสองชนิดคือโค้งคว่ำ(Crest) และโค้งหงาย(Sag)
สำหรับวิธีการคำนวณที่จะนำเสนอนี้จะใช้สูตรและวิธีการคำนวณแบบโค้งไม่สมมาตรเพียงอย่างเดียวเท่านั้น เพื่อให้ง่ายต่อการจำสูตรและนำไปใช้เขียนโปรแกรม ซึ่งสามารถนำไปคำนวณโค้งได้ทั้งแบบสมมาตรและแบบไม่สมมาตร
ส่วนประกอบโค้ง
PVC Point of Vertical Curve จุดเริ่มต้นโค้ง
PVI Point of Vertical Intersection จุดตัดของเส้นสัมผัสโค้งสองเส้น
PVT Point of Vertical Tangent จุดสิ้นสุดโค้ง
g1 Percent grade เปอร์เซ็นต์ความชันของเส้นสัมผัสโค้งจากจุด PVC ไปยัง PVI
g2 Percent grade เปอร์เซ็นต์ความชันของเส้นสัมผัสโค้งจากจุด PVI ไปยัง PVT
l1 ระยะจาก PVC ถึง PVI
l2 ระยะจาก PVI ถึง PVT
x ระยะทางจาก PVC ถึง sta ที่จะคำนวณที่อยู่ในช่วง l1
หรือระยะทางจาก PVT ถึง sta ที่จะคำนวณที่อยู่ในช่วง l2
y ระยะ Offset จากเส้นสัมผัสโค้งถึงเส้นโค้ง
e หรือ MO ระยะ Offset จากเส้นสัมผัสโค้งถึงเส้นโค้งที่จุด PVI
GT ค่าระดับบนเส้นสัมผัสโค้งที่จุดใดๆ
วิธีคำนวณ
ข้อมูลที่ต้องใช้ในการคำนวณได้แก่ค่า sta PVI, ค่าระดับที่ PVI, g1%, g2%, l1, l2
โดยทั่วไปแบบก่อสร้างจะกำหนดค่า l1, l2 มาให้สำหรับโค้งแบบไม่สมมาตร(Unsymmetrical)
แต่ในโค้งแบบสมมาตร(Symmetrical) จะกำหนดค่า L (หรือในแบบบางโครงการอาจใช้ตัวย่อ V.C.)มาให้ หาค่า l1, l2 ได้โดย
l1 = l2 = L÷2
สูตรที่ใช้คำนวณ

การหาค่าระดับที่ Sta ต่างๆ แบ่งเป็น 2 กรณีคือ
1. Sta อยู่ในช่วง l1 (Sta PVC ≤ Sta ≤ Sta PVI)


การหาจุดสูงสุดหรือต่ำสุดของโค้ง
จุดสูงสุด(Highest) หรือ ต่ำสุด(Lowest) ของโค้งจะเกิดขึ้นได้ใน 2 กรณีคือ
- g1>0 และ g2<0 จะเกิดจุดสูงสุด
- g1<0 และ g2>0 จะเกิดจุดต่ำสุด
สำหรับโค้งแบบสมมาตร ถ้า g1 = - g2 จุดต่ำสุดหรือจุดสูงสุดจะอยู่กลางโค้งที่ Sta PVI
เนื่องจากเรายังไม่ทราบว่า H/L(จุดต่ำสุดหรือจุดสูงสุด) อยู่ที่ตำแหน่งใดของโค้ง ไม่รู้ว่าอยู่ด้าน l1 หรือ l2 เราจะกำหนดตัวแปรขึ้นมาสองตัวเพื่อทดสอบว่า H/L อยู่ด้าน l1 หรือ l2
กำหนดให้
- x1 คือ ระยะจาก H/L ถึง Sta PVC
- x2 คือ ระยะจาก H/L ถึง Sta PVT
Sta H/L = Sta PVC + x1
แต่ถ้าค่า x1 > l1 แสดงว่า H/L อยู่เกินกว่าช่วง l1(อยู่ด้าน l2) ให้หาค่า x2 จาก
แล้วทำการหาค่า Sta H/L โดย
Sta H/L = Sta PVT - x2
ตัวอย่างการคำนวณ
ตัวอย่างที่ 1 กำหนดให้ Sta PVI 0+600.000 มีค่าระดับ 199.948, g1 = -1.486 %, g2 = -0.209 %, L=80 เมตร โดยคำนวณทุก 12.5 เมตร
- คำนวณส่วนประกอบโค้ง
(รูปแบบการเขียนแทนค่าสมการจะเขียนอยู่ในรูปไวยกรณ์ของ Fx-5800P เพื่อให้ง่ายต่อการกดเครื่องคิดเลขตาม)
โจทย์ให้ค่า L มา ดังนั้น l1 = l2 = 80÷2 = 40

- คำนวณค่าระดับบนโค้ง
คำนวณค่าระดับช่วง l1 โดย

ได้ผลลัพธ์ตามตาราง

คำนวณค่าระดับช่วง l2 โดย

ได้ผลลัพธ์ตามตาราง

- หาจุดสูงสุดหรือต่ำสุดของโค้ง
เนื่องจากค่า g1 และ g2 เป็นลบทั้งคู่ โค้งนี้จึงไม่มีสูงสุดหรือต่ำสุด
================================================
ตัวอย่างที่ 2 กำหนดให้ Sta PVI 10+260.000 มีค่าระดับ 195.948, g1 = -0.032 %, g2 = +4 %, L=130 เมตร โดยคำนวณทุก 12.5 เมตร
l1 = l2 = 130÷2 = 65
e = (4-(-0.032))x65x65÷(200(65+65)) = 0.6552
ได้ผลคำนวณตามตาราง
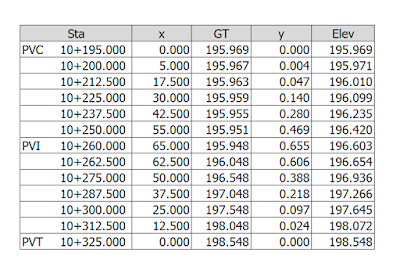
- หาจุดสูงสุดหรือต่ำสุดของโค้ง
g1 = -0.032, g2 = +4, l1 = 65, l2 = 65, e = 0.6552
g1 เป็นค่าลบ(-) g2 เป็นค่าบวก(+) ดังนั้นจะมี จุดต่ำสุด อยู่ในโค้ง
หาค่า
x1 = Abs(-0.032x652÷(200x0.6552)) = 1.032
เนื่องจาก x1 มีค่าน้อยกว่า l1 แสดงว่าจุดต่ำสุดอยู่ด้าน l1
∴ จุดต่ำสุดของโค้งอยู่ที่ Sta 10+195.000 + 1.032 = 10+196.032
มีค่าระดับ = 195.969 เมตร
Note : ฟังก์ชั่น Abs() บนเครื่องคิดเลข Casio Fx-5800P สามารถพิมพ์ได้โดยกด
ปุ่ม FUNCTION > 1:MATH > ปุ่มเลื่อนลง > 1:Abs
================================================
ตัวอย่างที่ 3 กำหนดให้ Sta PVI 23+450.000 มีค่าระดับ 275.014, g1 = -2.5 %, g2 = +1 %, l1 = 100, l2 = 80 โดยคำนวณทุก 25 เมตร
l1 ≠ l2 โค้งนี้เป็นโค้งแบบไม่สมมาตร (Unsymmetircal)
e = (1-(-2.5))x100x80÷(200(100+80)) = 0.7778
ได้ผลคำนวณตามตาราง

- หาจุดสูงสุดหรือต่ำสุดของโค้ง
g1 = -2.5, g2 = +1, l1 = 100, l2 = 80, e = 0.7778
g1 เป็นค่าลบ(-) g2 เป็นค่าบวก(+) ดังนั้นจะมี จุดต่ำสุด อยู่ในโค้ง
หาค่า
x1 = Abs(-2.5x1002÷(200x0.7778)) = 160.710
เนื่องจาก x1 มีค่ามากกว่า l1 แสดงว่าจุดต่ำสุดอยู่ด้าน l2
หาค่า
x2 = Abs(1x802÷(200x0.7778)) = 41.142
∴ จุดต่ำสุดของโค้งอยู่ที่ Sta 23+530.000 - 41.142 = 23+488.858
มีค่าระดับ = 275.608 เมตร
================================================
ตัวอย่างที่ 4 กำหนดให้ Sta PVI 0+425.000 มีค่าระดับ 202.548, g1 = +4 %, g2 = -1.486 %, V.C. = 200 โดยคำนวณทุก 25 เมตร
l1 = l2 = 200÷2 = 100
e = (-1.486-4)x100x100÷(200(100+100)) = -1.3715
ได้ผลคำนวณตามตาราง
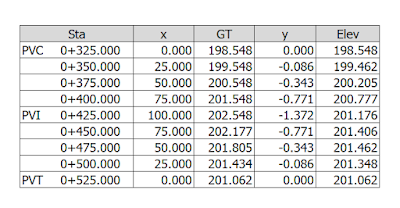
- หาจุดสูงสุดหรือต่ำสุดของโค้ง
g1 = +4, g2 = -1.486, l1 = 100, l2 = 100, e = -1.3715
g1 เป็นค่าบวก(+) g2 เป็นค่าลบ(-) ดังนั้นจะมี จุดสูงสุด อยู่ในโค้ง
หาค่า
x1 = Abs(4x1002÷(200x-1.3715)) = 145.826
เนื่องจาก x1 มีค่ามากกว่า l1 แสดงว่าจุดสูงสุดอยู่ด้าน l2
หาค่า
x2 = Abs(-1.486x1002÷(200x-1.3715)) = 54.174
∴ จุดสูงสุดของโค้งอยู่ที่ Sta 0+525.000 - 54.174 = 0+470.826
มีค่าระดับ = 201.465 เมตร
จบบท
Note :
ปัญหาอย่างนึงของคนหัดเขียนโปรแกรมคือการหาตัวอย่างเพื่อทดสอบการทำงานของโปรแกรม ผมลอง google ดูพบว่ามีตัวอย่างค่อนข้างน้อย ตัวอย่างของเว็บต่างประเทศส่วนใหญ่เป็นการรัน Sta แบบหน่วยฟุต บทนี้ก็เลยนำเสนอ 4 ตัวอย่าง พยายามให้ครอบคลุมทุกเงื่อนไขเพื่อใช้สำหรับทดสอบการทำงานของโปรแกรม
- ตัวอย่างที่ 1 เป็นโค้ง สมมาตร แบบ ไม่มีจุดสูงสุดหรือต่ำสุด
- ตัวอย่างที่ 2 เป็นโค้ง สมมาตร แบบมี จุดต่ำสุด อยู่ด้าน l1
- ตัวอย่างที่ 3 เป็นโค้ง ไม่สมมาตร แบบมี จุดต่ำสุด อยู่ด้าน l2
- ตัวอย่างที่ 4 เป็นโค้ง สมมาตร แบบมี จุดสูงสุด อยู่ด้าน l2




ยอดเยี่ยมค่ะ
ตอบลบ